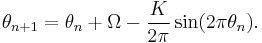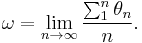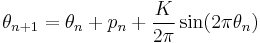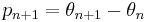Circle map
In mathematics, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors (specifically, a free-spinning wheel weakly coupled by a spring to a motor). The circle map equations also describe a simplified model of the phase-locked loop in electronics. The circle map exhibits certain regions of its parameters where it is locked to the driving frequency (phase-locking or mode-locking in the language of electronic circuits); these are referred to as Arnold tongues, after Vladimir Arnold. Among other applications, the circle map has been used to study the dynamical behaviour of a beating heart.
Contents |
Definition
The circle map is given by iterating the map
where  is to be interpreted as polar angle such that its value lies between 0 and 1.
is to be interpreted as polar angle such that its value lies between 0 and 1.
It has two parameters, the coupling strength K and the driving phase Ω. As a model for phase-locked loops, Ω may be interpreted as a driving frequency. For K = 0 and Ω irrational, the map reduces to an irrational rotation.
Mode locking
For small to intermediate values of K (that is, in the range of K = 0 to about K = 1), and certain values of Ω, the map exhibits a phenomenon called mode locking or phase locking. In a phase-locked region, the values 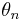 advance essentially as a rational multiple of n, although they may do so chaotically on the small scale.
advance essentially as a rational multiple of n, although they may do so chaotically on the small scale.
The limiting behavior in the mode-locked regions is given by the rotation number
which is also sometimes referred to as the map winding number.
The phase-locked regions, or Arnold tongues, are illustrated in black in the figure above. Each such V-shaped region touches down to a rational value 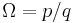 in the limit of
in the limit of 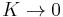 . The values of (K,Ω) in one of these regions will all result in a motion such that the rotation number
. The values of (K,Ω) in one of these regions will all result in a motion such that the rotation number 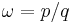 . For example, all values of (K,Ω) in the large V-shaped region in the bottom-center of the figure correspond to a rotation number of
. For example, all values of (K,Ω) in the large V-shaped region in the bottom-center of the figure correspond to a rotation number of 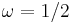 . One reason the term "locking" is used is that the individual values
. One reason the term "locking" is used is that the individual values 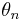 can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number. That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series
can be perturbed by rather large random disturbances (up to the width of the tongue, for a given value of K), without disturbing the limiting rotation number. That is, the sequence stays "locked on" to the signal, despite the addition of significant noise to the series 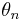 . This ability to "lock on" in the presence of noise is central to the utility of phase-locked loop electronic circuit.
. This ability to "lock on" in the presence of noise is central to the utility of phase-locked loop electronic circuit.
There is a mode-locked region for every rational number 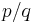 . It is sometimes said that the circle map maps the rationals, a set of measure zero at K = 0, to a set of non-zero measure for
. It is sometimes said that the circle map maps the rationals, a set of measure zero at K = 0, to a set of non-zero measure for 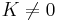 . The largest tongues, ordered by size, occur at the Farey fractions. Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω gives the "Devil's staircase", a shape that is generically similar to the Cantor function.
. The largest tongues, ordered by size, occur at the Farey fractions. Fixing K and taking a cross-section through this image, so that ω is plotted as a function of Ω gives the "Devil's staircase", a shape that is generically similar to the Cantor function.
The circle map also exhibits subharmonic routes to chaos, that is, period doubling of the form 3,6,12,24,....
Chirikov standard map
The Chirikov standard map is related to the circle map, having similar recurrence relations, which may be written as
with both iterates taken modulo 1. In essence, the standard map introduces a momentum 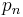 which is allowed to dynamically vary, rather than being forced fixed, as it is in the circle map. The standard map is studied in physics by means of the kicked rotor Hamiltonian.
which is allowed to dynamically vary, rather than being forced fixed, as it is in the circle map. The standard map is studied in physics by means of the kicked rotor Hamiltonian.
References
- Weisstein, Eric W., "Circle Map" from MathWorld.
- Philip L. Boyland : Bifurcations of circle maps: Arnol'd tongues, bistability and rotation intervals Comm. Math. Phys. Volume 106, Number 3 (1986), 353-381.
- Robert Gilmore and Marc Lefranc, The Topology of Chaos, Alice in Stretch and Squeezeland, (2002) Wiley Interscience ISBN 0-471-40816-6 (Provides a brief review of basic facts in section 2.12).
- Leon Glass, Michael R. Guevara, Alvin Shrier, Rafael Perez, "Bifurcation and Chaos in a Periodically Stimulated Cardiac Oscillator", Physica 7D (1983) pp 89–101. Bound as Order in Chaos, Proceedings of the International Conference on Order and Chaos held at the Center for Nonlinear Studies, Los Alamos, New Mexico 87545,USA 24–28 May 1982, Eds. David Campbell, Harvey Rose; North-Holland Amsterdam ISBN 0-444-86727-9. (Performs a detailed analysis of heart cardiac rhythms in the context of the circle map.)
- Mark McGuinness and Young Hong, Arnold tongues in human cardiorespiratory system, Chaos, March 2004, 14, 1.
External links
- Circle map with interactive Java applet